통계를 위한 수학을 논하려면 평균과 비율을 빼놓을 수 없다.
'평균이 뭐가 어렵다고 이걸 공부하고 있어?'
라고 생각하는 사람이 분명히 있을 것이고, 나 또한 그랬다.
Ⅰ. 평균

평균은 어지러운 수학의 세계에서도 내 마음을 평화롭게 만들어 주는 종류였으니까 말이다...
그런데도 굳이 평균에 대한 공부를 포스팅하는 이유는 그 의미가 남달라서 이기 때문이다.
학교에서 중간고사, 기말고사를 보고나서 많은 선생님, 교수님들은 평균을 논하는 걸 좋아하신다.
'너희 반이 다른 반보다 평균이 10점이나 더 낮구나, 어떻게 생각하니?'
라고 구박하시기도 하는데... 대체 평균에 어떤 의미가 있기에 평가의 기준이 된 것일까?
평균(平均)을 분해해 의미를 살펴보자면, 평평하게(平, 평평할 평) 고르는 것(均, 고를 균)이다.
국어사전에는
1. 여러 사물의 질이나 양 따위를 통일적으로 고르게 한 것.
2. 수학 여러 수나 같은 종류의 양의 중간값을 갖는 수.
라는 의미로 등재되어 있다.
[여담으로 average(평균)의 어원은 해상, 즉 바다 위에서 유래되었다고 한다.
중세 영주에게 보낼 곡물을 배위에 실어 나르곤 했는데
이때 바다 위의 태풍이나 거센 파도 등으로 곡물이 분실 혹은 손실되었을 경우
그에 대응하는 양만큼을 배의 주인이나 그 곡물의 주인들이 부담해야 했다.
즉, 분실되거나 손실된 물품을 공동으로 분담해서 부담해야 했는데
이 '공동 분담금'을 average라고 부른 것이다.]
평균이 새롭게 느껴지는가? 국어의 의미를 따지면서 점점 머릿속이 혼란스러워질 것이다.
평균을 천천히 처음부터 뜯어보도록 하자.
아래 각 높이가 8cm, 1cm, 3cm, 밑변이 1cm인 3개의 직사각형이 있다.

위의 그림을 직관적으로 이해할 수 있도록 변형시켜보겠다.
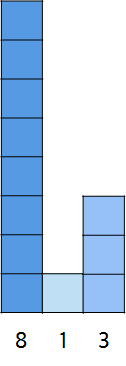
만약 이 직사각형들의 높이를 평평하게 만들어야 한다면 어떻게 하겠는가?
가장 긴 8을 쪼개어 1과 3으로 옮기면 높이가 평평해질 것이다.
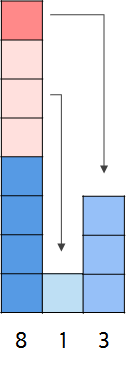
8을 1과 3, 4로 쪼개어 1을 높이가 3인 직사각형에게, 3을 높이가 1인 직사각형에게 준다면
높이가 4cm인 하나의 커다란 직사각형이 만들어진다.
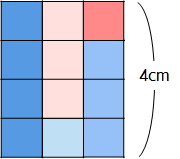
눈치 챘는가? 평평하게 만든 직사각형의 높이는 평균을 의미한다.
그리고 균일한 높이를 가지는 세 개의 직사각형을 합치면 커다란 직사각형의 면적이 된다.
즉, 높이(평균) X 개수 = 면적(합계) 가 되고
이를 정리하면 우리가 익히 알고 있는 평균의 식이 도출된다.
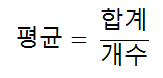
일반적으로 정리해보면 아래와 같다.
1부터 총 n개의 데이터가 있다고 하자.
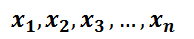
데이터의 합을 개수로 나눈 것이 평균이다.
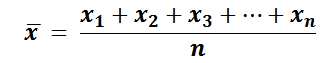
이제 평균을 왜 평균이라 부르고, 그 안의 의미를 어느정도 이해했을 것이다.
평균은 두 개 이상의 집단을 단순 비교할 때 자주 이용된다.
통계를 공부할 때도, 데이터마이닝을 공부할 때도, 혹은 그 외에도 '평균'을 자주 접하게 될 것이다.
그러나 평균을 가지고 놀다보면 범하게 되는 오류가 있는데 이는 예시를 통해 알아보겠다.
어벤져스팀과 저스티스리그팀이 있다고 하자.
어벤져스팀 구성원의 키는 각 170, 180, 240, 195, 175 이고
저스티스리그팀 구성원의 키는 각 195, 185, 180, 170, 190, 175이라고 할 때,
어벤져스팀의 평균 키는 195cm, 저스티스리그팀의 평균 키는 182.5cm이다.
그렇다면 어벤저스팀이 저스티스리그팀보다 크다고 할 수 있는가?
답은 '아니다'이다.
평균만으로는 알 수 없다.
어벤져스팀은 평균보다 키가 작은 사람이 3명이고 평균이 1명, 평균보다 큰 사람이 1명이다.
반면 저스티스리그팀은 평균보다 작은 사람이 3명, 평균보다 큰 사람이 3명이다.
어벤져스팀에는 키가 240cm인 거구의 초록색 거인이 있기 때문에 평균이 상대적으로 높다.
이처럼 평균으로는 확신할 수 없고, 알 수 없는 정보도 있으니 주의해야 한다.
데이터를 더 면밀히 탐색하기 위해 최빈값, 중앙값 등을 계산하기도 하는데 이는 다음에 알아보도록 하겠다.
Ⅱ. 비율
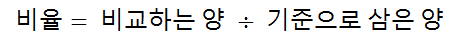
비율(rate)은 비교하는 양에서 기준으로 삼은 양을 나눈 값이다.

예를 들어 얼음마을에 사는 50마리의 황제펭귄 중 20마리가 춤을 춘다고 할 때,
얼음마을 펭귄의 40%가 춤을 춘다고 표현할 수 있다.
이때 기준으로 삼은 양은 얼음마을에 사는 50마리의 황제펭귄이고,
비교하는 양은 춤을 추는 20마리이다.
비율을 논할 때 '비'의 개념을 알고 있으면 이해가 수월해질 것이다.
비는 두 수의 양을 기호 ' : '를 사용하여 나타낸 것이며,
비와 비율 모두 둘 이상의 수를 비교할 때 사용한다.
이번엔 물감으로 예를 들어보자.
보라색의 물감을 만들기 위해서는 빨간색 물감과 파란색 물감을 같은 양으로, 즉 1 : 1로 섞으면 된다.
보라색에 붉은 색을 더 띄우고 싶다면 빨간색 물감을 두 배 많이 섞어 2 : 1 혹은 3 : 1의 비율로 조절해나가면 된다.
이때 각각의 양을 기호 ' : '로 나타낸 것을 '비'라고 한다.
A : B 는 A 대 B라고 읽으며
A는 비교하는 양, B는 기준으로 삼은 양을 뜻한다.
이때 B의 값이 100이라면 백분율(%)이 되는 것이다.
평균과 비율의 개념은 어렵지 않으나 데이터를 정리하고 분석할 때 자주 쓰인다.
특히 비율을 자유자재로 이용해야 할 때면 꽤나 난해하기 때문에 골머리를 앓을 수 있다.
내가 평균과 비율에 대해 포스팅을 하는 이유도 이러한 맥락에 따른 것인데,
로지스틱 회귀분석에서 다루는 오즈비가 갑작스럽게 느껴졌기 때문이다.
차후에 머리 아파올 때가 되면 이 포스팅으로 넘어와 잠시 쉬고 개념을 짚고 넘어가기를 바라며 글을 마친다.
※ 본 포스팅은 비전코리아 출판사의 『통계가 빨라지는 수학력』 을 참고하였습니다.
https://book.naver.com/bookdb/price.nhn?bid=10651826
book.naver.com